در یک مدل المان محدود می تواند نواحی وجود داشته باشد که با ریز کردن سایز المان ها در آن نواحی، حل به یک جواب منحصر به فرد همگرا نشود. نقاط با تکنیگی تنش جزو این نواحی محسوب می شوند. اصطلاحا به این نقاط، تنش تکین (stress singularity) گفته می شود. نقطه تنش تکین، نقطه ای از مش مدل المان محدود است که در آن تنش به مقدار مشخصی همگرا نمی شود. در واقع با افزایش چگالی مش در آن نقطه و در اطراف آن، تنش نیز افزایش می یابد. در نقاط سینگولار به لحاظ تئوریک، تنش به سمت بی نهایت میل می کند.
وجود مواردی مانند بار نقطه ای (point load) و گوشه های تیز (sharp corners) در هندسه سبب ایجاد نقاط سینگولار در مدل المان محدود می شود. با این که مقدار تنش در نقاط سینگولار درست نیست، اما این امر سبب زیر سوال بردن کل نتایج تحلیل المان محدود انجام شده نمی شود! اول از همه، با استفاده از یک مش مناسب، جابجایی های محاسبه شده حتی در نقاط سینگولار نیز درست محاسبه می شوند. تکینگی ایجاد شده سبب محاسبه اشتباه میدان تنش در خود نقطه تکین و در همسایگی نزدیک آن می شود. اما بر اساس اصل سنت ونان، در شعاع همسایگی خاصی به بعد نتایج بدست آمده برای میدان تنش کاملا درست محاسبه می شوند! در ادامه ضمن بر شمردن اصل سنت ونان، نحوه ایجاد، اثرات و نحوه تقابل با نواحی سینگولار را با هم بررسی می کنیم.
اصل سنت ونان (St.Venant’s Principle)
اصل سنت ونان بیان می کند که “تاثیر اغتشاشات محلی در یک میدان تنش یکنواخت، به صورت محلی باقی می ماند.” این اصل به شما اجازه می دهد تا در صورتی که مقدار تنش در نزدیکی و یا در خود نقاط سینگولار برایتان مهم نیست، بدون داشتن نگرانی از اثرات نقاط سینگولار بر روی سایر نقاطی که مقدار تنش در آن نقاط برایتان مهم است، از اثرات آنها صرف نظر کنید.
بار نقطه ای (point load)
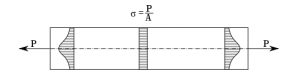
بر طبق شکل زیر، نمونه ساده ای را در نظر بگیرید که می خواهیم پاسخ آن به نیروی P را به صورت استاتیکی با یک نرم افزار المان محدود بررسی کنیم.
در شکل بالا، اعمال نیروی P به صورت نقطه ای سبب سینگولار شدن نقاط وسط هر کدام از دو طرف نمونه و در نتیجه خارج شدن پروفیل تنش از حالت یکنواخت در نزدیکی محل اعمال نیرو می شود. اما در فاصله به اندازه کافی دور از محل اعمال نیرو، پروفیل تنش کاملا یکنواخت می باشد. برای جلوگیری از ایجاد تکینگی (singularity)، می توانید به جای استفاده از نیروی نقطه ای، به لبه نمونه فشار (pressure load) وارد کنید . فشار سبب تکینگی نقطه ای (point singularity) نمی شود چراکه حلگر المان محدود فشار وارده را به طریقی تبدیل به مجموعه ای از نیرو های نقطه ای در طول گره های لبه نمونه می کند که از تکینگی نقطه ای جلوگیری می کند.
گوشه های تیز هندسه (sharp corners)
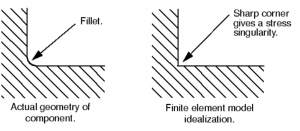
منظور از گوشه های تیز، گوشه هایی از مدل است که زاویه خارجی در آنها کمتر از ۱۸۰ درجه می باشد. در شکل زیر، زاویه خارجی گوشه نشان داده شده ۱۵۰ درجه می باشد. (زاویه صفر درجه بیان کننده نوک ترک می باشد)
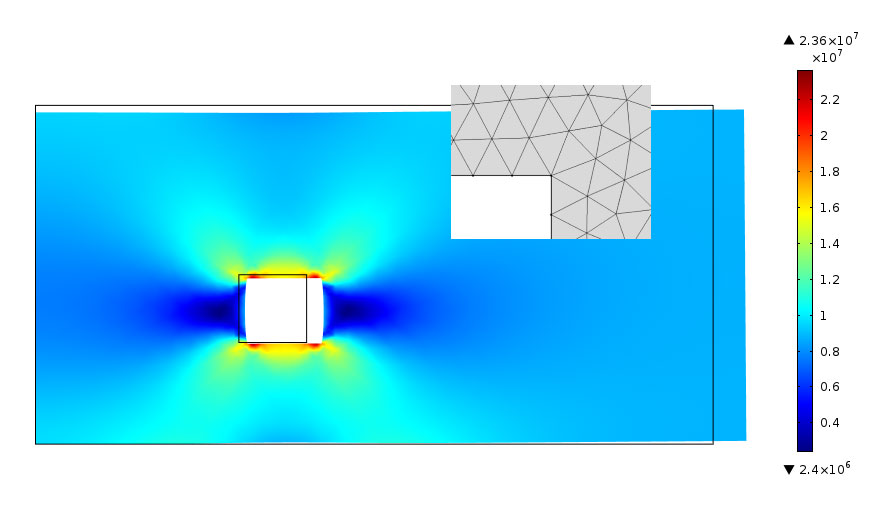
این گوشه یک نقطه تکین خواهد بود. در واقعیت هیچ گوشه ای نمی تواند کاملا تیز باشد و اگر در یک قطعه تولید شده گوشه تیز وجود داشته باشد، این گوشه همواره دارای فیلت (fillet) با شعاع کوچک خواهد بود. این امر نشان می دهد که هیچ گاه در واقعیت تنش به سمت بی نهایت میل نمی کند. اما وجود گوشه تیز می تواند سبب تمرکز تنش بشود. به منظور محاسبه دقیق مقدار تنش در نقاط تمرکز تنش باید سایز المان ها به صورت محلی و در حوالی این نقاط ریز شود. برای مثال در اطراف سوراخی که در هندسه مدل وجود دارد، باید در ناحیه ای به اندازه قطر سوراخ فاصله از مرکز سوراخ، سایز المان ها ریز شود . ریز کردن سایز المان ها در سایر نواحی نه تنها اثر چندانی بر دقت محاسبه ندارد بلکه بدون هر گونه فایده ای سبب افزایش شدید حجم محاسبات می شود.
نحوه تقابل با نقاط سینگولار
در صورتی که هدف از انجام آنالیز محاسبه مقدار دقیق تنش در نزدیکی هیچ کدام از نقاط سینگولار (گوشه های تیز و نقاطی که بار به صورت نقطه ای وارد شده است) نباشد، با توجه به اصل سنت ونان، بدون نگرانی از وجود این نقاط می توان شبیه سازی را انجام داد و به نتایج شبیه سازی استناد کرد. البته مقدار جابجایی ها حتی در خود نقاط سینگولار همواره بدرستی محاسبه می شود. همچنین مقدار انتگرال تنش روی همسایگی نزدیک به نقاط سینگولار نیز همواره دقیق خواهد بود. در صورت لحاظ نمودن تمام شعاع انحنا های هر اندازه کوچک و اعمال بار های نقطه ای به صورت فشار با اندازه بالا و استفاده از مش با سایز ریز در حوالی نقاط نامبرده عملا میدان تنش محاسبه شده حتی در همسایگی نزدیک این نقاط نیز قابل استناد خواهد بود. در حقیقت با حذف تمام ایده آل سازی های فیزیکی (مانند مدل سازی نقاط گیردار (clamped) با بستن تمام درجات آزادی گره های اتصال و عدم استفاده از اتصال تغییر شکل پذیر ) و هندسی از مدل المان محدود، تکینگی تنش از نتایج حل حذف می شود. در شکل زیر نمونه ای از ایده آل سازی هندسی مدل که به آن اصطلاحا عملیات “defeaturing” نیز گفته می شود، آورده شده است.
جمع بندی
همواره به دلیل ایده آل سازی مساله و کاهش پیچیدگی های هندسی، نقاط سینگولار پدید می آیند. با توجه به اصل سنت ونان، تنها باید در نقاطی که مقدار تنش دارای اهمیت است از ایده آل سازی های فیزیکی و هندسی (defeaturing) پرهیز شود و به منظور کاهش پیچیدگی و نیز کاهش حجم محاسبات می توان در سایر نقاط از ایده آل سازی استفاده کرد.
مراجع:











عالی بود
سلام . خیلی ممنونم از لطفتون .
سلام.
بسیار عالی است. متشکرم.
سلام . خواهش می کنم . خوشحالم که مطلب براتون مفید بوده .